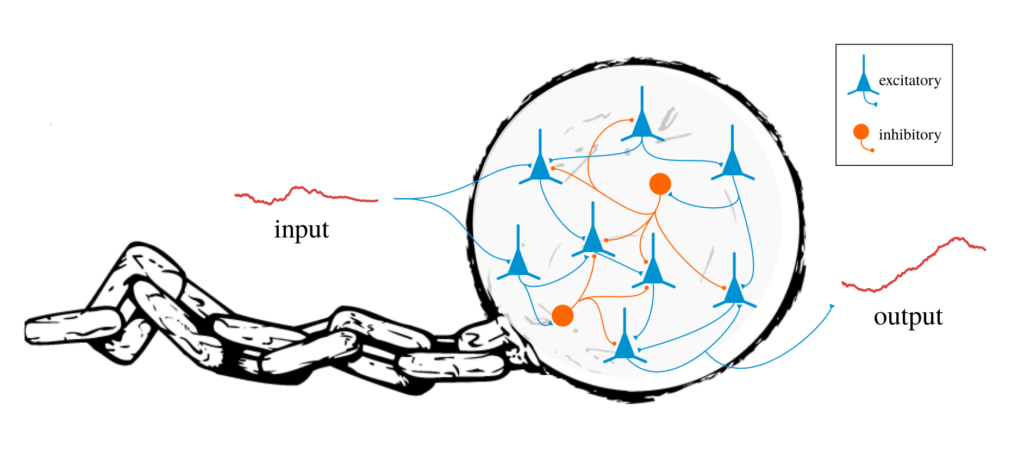
Computation is usually conceptualized in terms of input/output functions. For instance, to compute the square root of a number is to somehow solve the function that takes a number as an input and outputs its square root. It is commonly stated that feed-forward neural networks are “universal approximators” meaning that, in theory, any function can be approximated by a feed-forward neural network. Here are some examples of this idea being articulated:
“One of the most striking facts about [feed-forward] neural networks is that they can compute any function at all.”
– Neural Networks and Deep Learning, Ch. 4, Michael Nielsen
“In summary, a feed-forward network with a single layer is sufficient to represent any function [to an arbitrary degree of accuracy],…”
– Deep Learning (Section 6.4.1 Universal Approximation Properties and Depth), Ian Goodfellow
“…but can we solve anything? Can we stave off another neural winter coming from there being certain functions that we cannot approximate? Actually, yes. The problem of not being able to approximate some function is not going to come back.”
–Course on Deep Learning, Universal Approximation Theorem, Konrad Kording
Continue reading “The Truth About the [Not So] Universal Approximation Theorem”